Prédire les valeurs manquantes
Valeurs manquantes
Dès lors qu’on est amené à collecter et analyser des données, on est rapidement confronté au problème de données manquantes.
Que faire ?
Il y a différentes possibilités pour traiter ces données manquantes, en fonction du problème, du type de données, du volume, etc.
Par exemple :
- Supprimer les observations avec les données manquantes (attention si elle ne sont pas manquantes aléatoirement)
- Imputer les manquants avec la valeur moyenne, médiane etc
- Pour des séries temporelles, imputer avec la dernière valeurs, ou la prochaine
- La valeur manquante peut être une information en soit, il est alors intéressant de conserver l’information pour analyser les données en créant une nouvelle variable par exemple manquant oui/non.
- Créer un algorithme pour prédire la valeur manquante à l’aide des valeurs des autres variables.
Dans ce post, je vais décrire la dernière méthode, montrer comment utiliser le deep learning pour prédire les valeurs manquantes d’un jeu de données, contenant un million d’observations avec un millions de manquants répartis sur un ensemble de variables.
Je vais pour cela utiliser les données provenant de Kaggle pour la compétition du mois de juin 2022.
Note : J’utiliserai indépendamment valeur manquante ou NA (not available)
Vous pouvez trouver les données à l’adresse suivante : https://www.kaggle.com/competitions/tabular-playground-series-jun-2022/data
Exploration des données
Le jeu de données se composent de 80 variables (plus un id), réparties en 4 groupes F_1*, F_2*, F_3* et F_4*.
skimr::skim(data) skim_variable n_missing complete_rate mean sd p0 p25 p50 p75 p100 hist
1 row_id 0 1 5.00e+5 288675. 0 250000. 5.00e+5 749999. 999999 ▇▇▇▇▇
2 F_1_0 18397 0.982 -6.87e-4 1.00 -4.66 -0.675 -7.69e-4 0.673 5.04 ▁▂▇▂▁
3 F_1_1 18216 0.982 2.09e-3 1.00 -4.79 -0.672 2.05e-3 0.676 5.04 ▁▂▇▂▁
4 F_1_2 18008 0.982 5.51e-4 1.00 -4.87 -0.674 1.39e-3 0.674 5.13 ▁▂▇▂▁
5 F_1_3 18250 0.982 9.82e-4 1.00 -5.05 -0.672 3.7 e-4 0.675 5.46 ▁▂▇▁▁
6 F_1_4 18322 0.982 2.44e-3 1.00 -5.36 -0.672 2.73e-3 0.677 4.86 ▁▁▇▂▁
7 F_1_5 18089 0.982 6.35e-4 1.00 -5.51 -0.674 2.76e-4 0.676 4.96 ▁▁▇▂▁
8 F_1_6 18133 0.982 -1.24e-4 1.00 -5.20 -0.675 8.14e-4 0.674 4.96 ▁▂▇▂▁
9 F_1_7 18128 0.982 -6.39e-2 0.726 -6.99 -0.500 5.78e-4 0.444 2.53 ▁▁▁▇▂
10 F_1_8 18162 0.982 -1.38e-5 1.00 -4.57 -0.674 -4.7 e-5 0.674 4.89 ▁▂▇▂▁
11 F_1_9 18249 0.982 4.51e-4 1.00 -5.00 -0.674 1.12e-3 0.676 4.79 ▁▂▇▂▁
12 F_1_10 17961 0.982 1.85e-4 0.999 -4.79 -0.674 6.71e-4 0.674 4.91 ▁▂▇▂▁
13 F_1_11 18170 0.982 -1.13e-3 1.00 -4.61 -0.677 -1.29e-3 0.674 4.82 ▁▂▇▂▁
14 F_1_12 18203 0.982 -6.12e-2 0.712 -7.06 -0.489 5.47e-4 0.436 2.30 ▁▁▁▇▃
15 F_1_13 18398 0.982 -6.71e-2 0.746 -6.90 -0.514 -8.04e-4 0.455 2.54 ▁▁▁▇▂
16 F_1_14 18039 0.982 -9.05e-4 1.00 -4.63 -0.676 -1.61e-4 0.673 4.82 ▁▂▇▂▁
17 F_2_0 0 1 2.69e+0 1.88 0 1 2 e+0 4 15 ▇▃▁▁▁
18 F_2_1 0 1 2.51e+0 1.75 0 1 2 e+0 4 14 ▇▆▁▁▁
19 F_2_2 0 1 9.77e-1 1.04 0 0 1 e+0 2 11 ▇▁▁▁▁
20 F_2_3 0 1 2.52e+0 1.65 0 1 2 e+0 4 14 ▇▆▁▁▁
21 F_2_4 0 1 2.94e+0 1.98 0 1 3 e+0 4 16 ▇▃▁▁▁
22 F_2_5 0 1 1.53e+0 1.35 0 1 1 e+0 2 12 ▇▂▁▁▁
23 F_2_6 0 1 1.49e+0 1.32 0 0 1 e+0 2 12 ▇▂▁▁▁
24 F_2_7 0 1 2.65e+0 1.74 0 1 2 e+0 4 16 ▇▃▁▁▁
25 F_2_8 0 1 1.18e+0 1.32 0 0 1 e+0 2 13 ▇▁▁▁▁
26 F_2_9 0 1 1.11e+0 1.10 0 0 1 e+0 2 11 ▇▁▁▁▁
27 F_2_10 0 1 3.28e+0 1.87 0 2 3 e+0 4 17 ▇▅▁▁▁
28 F_2_11 0 1 2.47e+0 1.60 0 1 2 e+0 3 13 ▇▆▁▁▁
29 F_2_12 0 1 2.76e+0 1.70 0 2 3 e+0 4 15 ▇▃▁▁▁
30 F_2_13 0 1 2.48e+0 1.65 0 1 2 e+0 3 15 ▇▂▁▁▁
31 F_2_14 0 1 1.72e+0 1.56 0 1 1 e+0 3 13 ▇▂▁▁▁
32 F_2_15 0 1 1.78e+0 1.46 0 1 2 e+0 3 13 ▇▃▁▁▁
33 F_2_16 0 1 1.80e+0 1.46 0 1 2 e+0 3 13 ▇▃▁▁▁
34 F_2_17 0 1 1.24e+0 1.25 0 0 1 e+0 2 12 ▇▁▁▁▁
35 F_2_18 0 1 1.56e+0 1.44 0 0 1 e+0 2 15 ▇▁▁▁▁
36 F_2_19 0 1 1.60e+0 1.42 0 0 1 e+0 2 13 ▇▂▁▁▁
37 F_2_20 0 1 2.23e+0 1.56 0 1 2 e+0 3 14 ▇▅▁▁▁
38 F_2_21 0 1 2.03e+0 1.61 0 1 2 e+0 3 15 ▇▂▁▁▁
39 F_2_22 0 1 1.61e+0 1.56 0 0 1 e+0 2 16 ▇▁▁▁▁
40 F_2_23 0 1 7.09e-1 1.08 0 0 0 1 11 ▇▁▁▁▁
41 F_2_24 0 1 3.13e+0 1.82 0 2 3 e+0 4 17 ▇▅▁▁▁
42 F_3_0 18029 0.982 1.74e-3 1.00 -4.69 -0.675 3.25e-3 0.677 4.59 ▁▂▇▂▁
43 F_3_1 18345 0.982 -1.15e-3 1.00 -4.47 -0.675 4.81e-4 0.674 4.85 ▁▃▇▂▁
44 F_3_2 18056 0.982 6.05e-4 0.999 -4.89 -0.673 3.92e-4 0.675 4.76 ▁▂▇▂▁
45 F_3_3 18054 0.982 8.34e-4 1.00 -4.68 -0.674 8.54e-4 0.676 4.99 ▁▂▇▂▁
46 F_3_4 18373 0.982 1.29e-3 1.00 -5.01 -0.673 2.64e-3 0.677 4.72 ▁▂▇▂▁
47 F_3_5 18298 0.982 -2.18e-3 1.00 -4.87 -0.676 -1.60e-3 0.672 5.04 ▁▂▇▂▁
48 F_3_6 18192 0.982 5.78e-5 0.999 -5.02 -0.675 8.54e-4 0.673 4.53 ▁▂▇▃▁
49 F_3_7 18013 0.982 1.52e-3 1.00 -5.05 -0.673 1.20e-3 0.676 5.46 ▁▂▇▁▁
50 F_3_8 18098 0.982 7.73e-4 1.00 -5.51 -0.676 -1.95e-5 0.676 5.11 ▁▁▇▂▁
51 F_3_9 18106 0.982 -4.40e-4 1.00 -4.85 -0.675 -1.77e-3 0.674 5.10 ▁▂▇▂▁
52 F_3_10 18200 0.982 1.71e-3 1.00 -4.63 -0.672 1.57e-3 0.675 5.13 ▁▃▇▁▁
53 F_3_11 18388 0.982 7.33e-4 0.999 -4.60 -0.675 4.80e-4 0.675 4.68 ▁▂▇▂▁
54 F_3_12 18297 0.982 2.59e-4 1.00 -4.53 -0.674 1.83e-3 0.674 4.94 ▁▃▇▂▁
55 F_3_13 18060 0.982 -2.46e-3 1.00 -4.75 -0.676 -1.59e-3 0.674 4.71 ▁▂▇▂▁
56 F_3_14 18139 0.982 7.27e-4 0.999 -5.36 -0.673 1 e-4 0.674 4.82 ▁▁▇▃▁
57 F_3_15 18238 0.982 -1.51e-3 1.00 -4.45 -0.675 -1.36e-3 0.674 5.25 ▁▃▇▁▁
58 F_3_16 18122 0.982 -6.65e-4 1.00 -4.82 -0.675 -1.70e-3 0.675 4.84 ▁▂▇▂▁
59 F_3_17 18278 0.982 -2.14e-4 1.00 -4.81 -0.675 -4.14e-4 0.674 5.06 ▁▂▇▂▁
60 F_3_18 18089 0.982 6.27e-5 1.00 -5.20 -0.674 1.63e-4 0.675 4.96 ▁▂▇▂▁
61 F_3_19 18200 0.982 -6.49e-2 0.739 -6.07 -0.507 6.76e-4 0.451 2.67 ▁▁▂▇▁
62 F_3_20 18248 0.982 2.37e-3 0.999 -5.00 -0.671 2.45e-3 0.676 6.03 ▁▃▇▁▁
63 F_3_21 18396 0.982 -5.93e-2 0.697 -7.15 -0.480 -6.49e-4 0.428 2.39 ▁▁▁▇▂
64 F_3_22 18177 0.982 8.73e-5 0.999 -4.74 -0.674 5.9 e-5 0.674 4.97 ▁▂▇▂▁
65 F_3_23 18206 0.982 3.65e-4 1.00 -5.25 -0.674 -4.52e-4 0.675 4.81 ▁▁▇▂▁
66 F_3_24 18145 0.982 -8.17e-4 1.00 -4.89 -0.675 -4.57e-4 0.674 4.98 ▁▂▇▂▁
67 F_4_0 18128 0.982 3.27e-1 2.32 -12.9 -1.17 4.21e-1 1.91 10.7 ▁▁▇▅▁
68 F_4_1 18164 0.982 -3.31e-1 2.41 -12.5 -1.96 -3.56e-1 1.28 11.7 ▁▂▇▂▁
69 F_4_2 18495 0.982 -8.58e-2 0.837 -9.66 -0.608 -6.20e-2 0.485 2.91 ▁▁▁▇▃
70 F_4_3 18029 0.982 -1.95e-1 0.821 -9.94 -0.686 -1.37e-1 0.369 2.58 ▁▁▁▇▅
71 F_4_4 17957 0.982 3.33e-1 2.37 -12.8 -1.19 4.25e-1 1.94 11.9 ▁▁▇▃▁
72 F_4_5 18063 0.982 3.36e-1 2.35 -12.5 -1.27 3.03e-1 1.92 13.5 ▁▂▇▁▁
73 F_4_6 18325 0.982 3.77e-3 2.29 -11.1 -1.57 -7.18e-2 1.52 11.5 ▁▂▇▂▁
74 F_4_7 18014 0.982 3.34e-1 2.36 -11.7 -1.22 3.79e-1 1.93 12.5 ▁▂▇▂▁
75 F_4_8 18176 0.982 -7.18e-2 0.778 -10.1 -0.518 1.82e-2 0.475 2.61 ▁▁▁▇▇
76 F_4_9 18265 0.982 -7.99e-2 0.807 -9.86 -0.577 -2.78e-2 0.480 2.81 ▁▁▁▇▅
77 F_4_10 18225 0.982 3.83e-2 0.707 -10.4 -0.386 1.03e-1 0.530 2.55 ▁▁▁▆▇
78 F_4_11 18119 0.982 5.52e-1 5.00 -26.3 -2.79 2.03e-1 3.65 31.2 ▁▂▇▁▁
79 F_4_12 18306 0.982 3.34e-1 2.38 -11.5 -1.27 3.54e-1 1.95 11.3 ▁▂▇▂▁
80 F_4_13 17995 0.982 3.30e-1 2.36 -10.7 -1.30 2.95e-1 1.92 11.9 ▁▂▇▂▁
81 F_4_14 18267 0.982 3.72e-2 0.776 -9.98 -0.396 1.31e-1 0.574 2.58 ▁▁▁▇▇Toutes les variables sont continues à l’exception des variables F_2* qui ne contiennent pas de données manquantes. On doit donc prédire les manquants pour des données continues, c’est un problème de régression.
Chaque variable contient à peu près la même proportion de manquant 1.8%.
Comment sont-elles réparties ?
data$count_na <- rowSums(is.na(data))
data %>%
count(count_na, sort = TRUE) count_na n
<dbl> <int>
1 1 370798
2 0 364774
3 2 185543
4 3 61191
5 4 14488
6 5 2723
7 6 413
8 7 64
9 8 4
10 9 2Il y a 364774 observations sans manquants, 370798 avec un seul NA, et jusqu’à 9 Na pour une même observation.
Une stratégie peut commencer à se dessiner ici, qui consisterai à utiliser les 364774 observations sans manquants entrainer l’algorithme et prédire les 370798 avec manquants. Le problème sera plus complexe à partir de 2 manquants car ils ne seront probablement pas répartis sur les mêmes variables.
Si on regarde les combinaisons de manquants, il y a 42633 combinaisons possibles. Il va donc falloir simplifier le problème. Poussons un peu l’analyse.
Visualisons les corrélations :
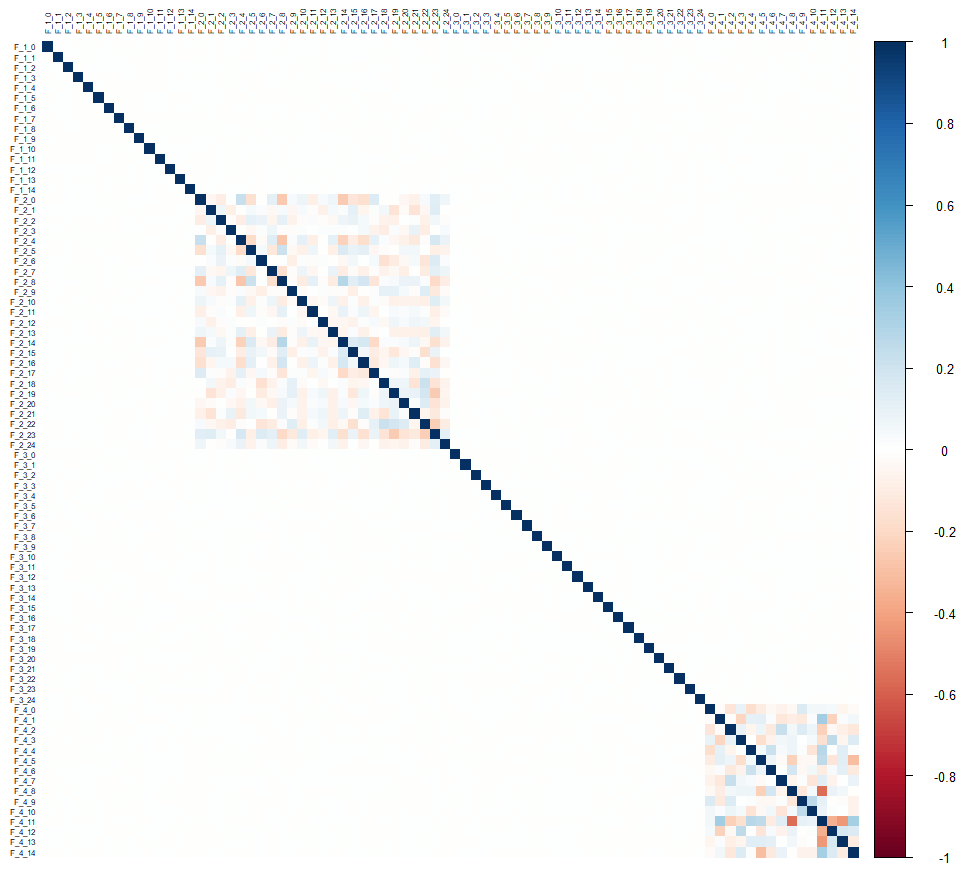
corrplot::corrplot(cor(drop_na(data[,-1])), tl.cex = 0.5, tl.col = "black", method = "color")En regardant la matrice de corrélation, on s’aperçoit qu’il n’y a aucune corrélation entre les groupes de variables, et seuls les groupes F_2 et F_4 présentent des corrélations mais uniquement internes au groupe.
Ça laisse à penser qu’il va être difficile de prédire les variables F_1* et F_3*, et que les variables F_2* ne seront probablement pas d’une grande aide.
Un moyen de le confirmer, est de créer un premier algorithme pour prédire ces variables lorsqu’il n’y a qu’un seul manquant. J’ai donc créé rapidement un algorithme qui boucle sur chaque variable, et créé un modèle (avec LightGBM) par variable à prédire. On s’aperçoit tout de suite qu’il n’y parvient pas, et ce pour chacune des variables F_1* et F_3*.
On voit tout de suite que le RMSE augmente pour les données de validation au lieu de diminuer :
[1]: train's rmse:0.99907 valid's rmse:0.999992
[11]: train's rmse:0.983548 valid's rmse:1.00045
[21]: train's rmse:0.968703 valid's rmse:1.00171
[31]: train's rmse:0.954811 valid's rmse:1.00238
[41]: train's rmse:0.941672 valid's rmse:1.00242
[51]: train's rmse:0.929105 valid's rmse:1.00233
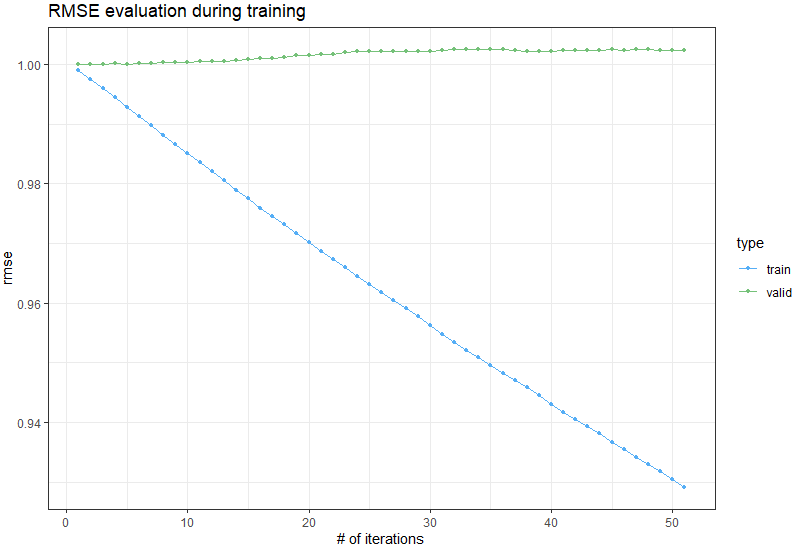
Et en traçant l’évolution du RMSE pour train et valid :
On voit clairement sur les données de validations que les prédictions se dégradent.
La meilleure stratégie pour les variables F_1* et F_3* est d’imputer avec leurs moyennes, après quelques tests, c’est ce qui donne le meilleur résultat. 40 variables peuvent donc être traitées de façon très simple.
Voir le code pour l’imputation avec la moyenne ou la médiane sur github.
Il ne reste qu’à trouver une solution pour les variables F_4*, qui ne sont plus qu’au nombre de 15.
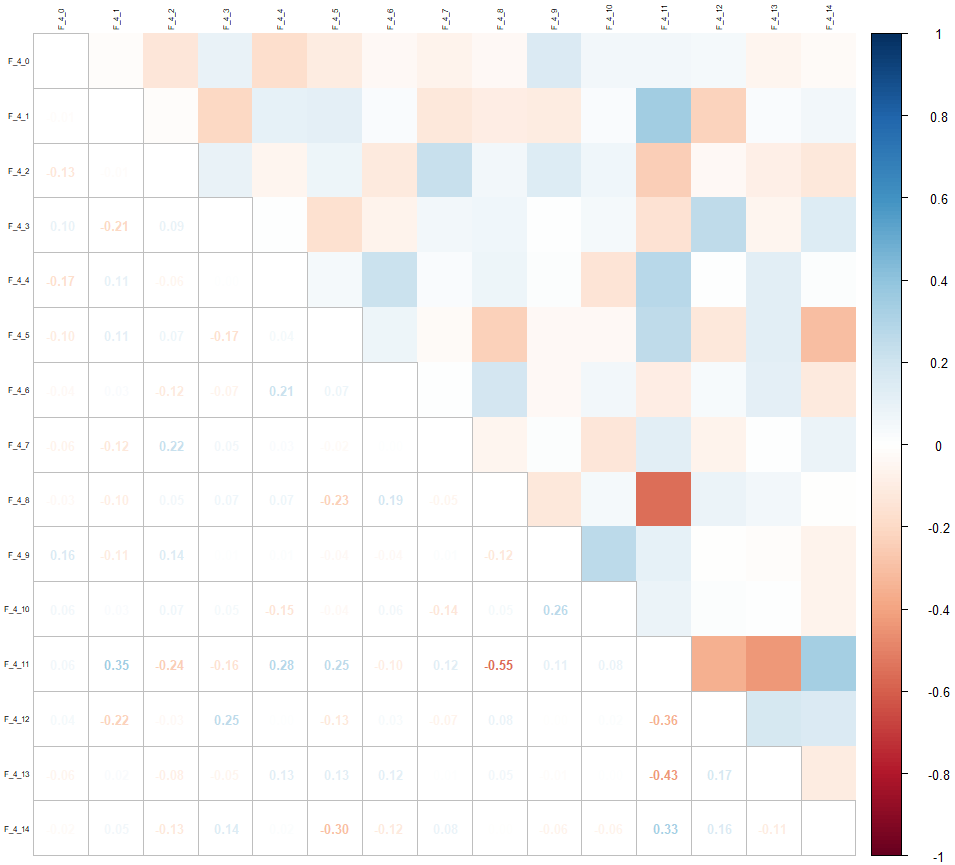
Regardons à nouveau la matrice de corrélation uniquement pour ces variables :
corrplot::corrplot(cor(drop_na(select(data, contains("F_4")))), tl.cex = 0.5, tl.col = "black", method = "square", type = "upper")
corrplot::corrplot.mixed(cor(drop_na(select(data, contains("F_4")))), tl.cex = 0.5, tl.col = "black", tl.offset = 0.2, upper = "color", number.cex = 0.8, tl.pos = "lt")On réévalue les manquants uniquement pour ces variables :
count_na n
<dbl> <int>
1 0 759268
2 1 211342
3 2 27127
4 3 2124
5 4 135
6 5 4On n’a plus qu’un maximum de 5 manquants par observation, et une proportion de données complètes pour entrainer l’algorithme de 76%.
Bien entendu lorsqu’il y a plus d’un manquant, ils peuvent être répartis sur 14 variables, ce qui donne dans notre cas 703 combinaisons.
Par exemple, pour prédire les manquants de la variable F_4_0, on peut n’avoir aucune autre manquant, ou un manquant sur la variable F_4_2, ou sur la variable F_4_3, ou encore 2 autres manquants, sur les variables F_4_3 et F_4_5 etc.
Stratégies
Stratégie 1 : Prédiction par variable
Le principe est d’utiliser un algorithme qui sait faire des prédictions malgré des valeurs manquantes, comme LightGBM. On créé un modèle par variable à prédire, qu’on entraine sur les données qui n’ont pas de manquants
On prédit toutes les valeurs manquantes de cette variable indépendamment du fait qu’il puisse manquer des valeurs sur d’autres variables. Bien entendu, plus il y a de valeurs manquantes, plus la prédiction va être mauvaise. On peut jouer sur certains paramètres de lightGBM pour améliorer la tolérance aux manquants comme feature_fraction qui permet de réduire le nombre de variables utilisées pour chaque arbre de décision. C’est à double tranchant, car ça peut réduire la performance pour les observations complètes. Il faut donc trouver la bonne valeur du paramètre par hyperparameter tuning.
Pour améliorer les prédictions, on peut compléter par un réseau de neurones : on utilise alors un deuxième data frame dont les valeurs manquantes ont été remplacées par celle prédites par lightGBM (les réseaux de neurones ne peuvent pas gérer les NA).
- Avantages : on ne créé que 15 modèles, c’est donc assez rapide, le RMSE est de 0.86 ce qui est correct
- Inconvénients : les prédictions de lightGBM sont plus imprécises lorsqu’il y a des manquants, et ces valeurs sont utilisées par le réseau de neurones, on peut donc amplifier l’incertitude et la marge d’amélioration est faible.
Stratégie 2 : Altérer les données d’entrainement pour ajouter des manquants
Cette stratégie a été proposée par un des compétiteurs sur Kaggle. Il s’agit de remplacer les NA par une valeur (-1 mais on peut choisir autre chose) pour les variables indépendantes afin de pouvoir utiliser le deep learning. Mais bien sur on ne pourra pas faire de prédiction si ces valeurs n’ont pas été vues au préalable lors de la phase d’entrainement. Il faut donc altérer les données d’entrainement pour remplacer de vrais données aléatoirement par des -1.
Pour que ça fonctionne, il faut ajouter autant de -1 qu’il y a de NA, donc on créé des modèles par nombre de NA dans les variables indépendantes. Par exemple s’il y a 2 variables indépendantes avec NA, on créé pour chaque observation des données d’entrainements, 2 valeurs -1 qu’on répartit aléatoirement entre les variables en s’assurant qu’il n’y en ait que 2 NA par observation.
- Avantages : ca améliore légèrement les prédictions
- Inconvénients : C’est plus complexe à coder (en particulier pour attribuer aléatoirement les -1 en fonction du nombre de NA), et plus long à entrainer.
Stratégie 3 : Prédire plusieurs variables simultanément (régression avec plusieurs sorties)
C’est la stratégie qui a donné de meilleur résultat et que je vais développer ensuite dans ce post.
L’idée ici est de prédire pour chaque combinaison de manquant, un modèle qui aura autant de sorties que de manquants pour prédire tous les manquants simultanément.
C’est finalement assez facile à faire, car il s’agit de créer un réseau de neurone avec autant de neurones qu’il y a de NA pour la couche de sortie.
Mise en oeuvre
Pour pouvoir appliquer cette stratégie, il faut grouper les données par combinaison de valeur manquantes. On créé donc une variable qui liste des noms des variables contenant des NA pour chaque observation.
list_variables <- colnames(data)
list_cols <- list_variables[grep("F_4",list_variables)]
data <- data %>%
select(row_id, all_of(list_cols))On créé une fonction na_col() qui crée une nouvelle variable contenant le nom de la variable si la valeur de la variable d’origine est NA, ou vide sinon.
na_col <- function(var, data){
var_ts <- sym(var)
new_var_ts <- sym(glue::glue(var, "_na"))
data %>%
select({{var_ts}}) %>%
mutate("{{new_var_ts}}" := ifelse(is.na({{var_ts}}), var, "")) %>%
select(-{{var_ts}})
}On utilise map_dfr() et reduce() du package {purrr} pour appliquer la fonction na_col() à toutes les variables et obtenir une seule variable avec la liste de toutes les variables contenant des NAs par observation.
data_mut <- map_dfc(list_cols, na_col, data) %>%
mutate(na_cols = reduce(., paste, sep = " ")) %>%
mutate(na_cols = str_squish(na_cols))
data <- data %>%
bind_cols(select(data_mut, na_cols))
data$cnt <- rowSums(is.na(data)) # nb NA Explication :
map_dfc()applique la fonctionna_col()sur toutes les variables et retourne un dataframe contenant autant de colonnes qu’il y a de variables, et contenant le nom de la variable si sa valeur est NA, ou vide sinon.reduce()combiné àpaste, permet de ne créer qu’une seule variable contenant la concaténation de toutes ces valeurs.str_squish()supprime tous les espaces en trop, pour ne conserver que les séparateurs.
On a donc à présent un dataframe contenant uniquement les variables F_4_* ainsi que la variable na_cols, qui contient la liste des variables contenant des NA, séparées par un espace, et la variable cnt qui contient le nombre de NA par observation.
Regardons un aperçu du nombre de combinaisons uniques :
unique_combi <- unique(data$na_cols)[-1]
head(unique_combi, 20) [1] "F_4_2" "F_4_4" "F_4_3 F_4_14" "F_4_12" "F_4_14" "F_4_3" "F_4_8 F_4_12" "F_4_1" "F_4_8 F_4_14"
[10] "F_4_8" "F_4_4 F_4_14" "F_4_5" "F_4_9" "F_4_2 F_4_13" "F_4_10" "F_4_3 F_4_13" "F_4_0" "F_4_7 F_4_9"
[19] "F_4_6" "F_4_13"
On utilise ensuite la partie du dataframe ne contenant aucun NA pour entrainer l’algorithme, avec un split pour avoir des données d’entrainement et de validation.
train_basis <- data %>%
filter(cnt == 0) %>%
select(-na_cols, -cnt)
split <- floor(0.80*NROW(train_basis))On peut ensuite boucler sur toutes les combinaisons de variables pour créer autant de modèles qu’il y a de combinaisons. Cependant, au vu du nombre de modèle à créer, il est préférable de boucler par variable à prédire, et ensuite par combinaison comprenant cette variable, ce qui permet d’exécuter plusieurs modèles en parallèle. C’est ce que permet cette structure :
for(variable in list_cols){
combi_var <- unique_combi[str_detect(unique_combi, variable)]
for(combi in combi_var){
set_cols <- str_split(combi, " ", simplify = TRUE)[,1]
# ** MODEL **
}
}La variable set_cols contient la liste des colonnes contenant des NA pour cette itération de la boucle.
On peut donc se concentrer sur le modèle.
Les données d’entrainement contiennent toutes les colonnes ne contenant pas de manquant, et la cible est une matrice contenant les valeurs pour les différentes variables à prédire (celles contenues dans set_cols)
train_df <- train_basis[1:split,] %>%
select(-all_of(set_cols), -row_id)
train_target <- train_basis[1:split,] %>%
select(all_of(set_cols)) %>%
as.matrix()On fait de même pour les données de validations :
valid_df <- train_basis[split:NROW(train_basis),] %>%
select(-all_of(set_cols), -row_id)
valid_target <- train_basis[split:NROW(train_basis),] %>%
select(all_of(set_cols)) %>%
as.matrix()Et enfin on prépare les données de test en filtrant uniquement les données contenant des NA pour cette combinaison de variable, et en ne sélectionnant que les variables qui n’ont pas de manquant :
test_df <- data %>%
filter(na_cols %in% combi) %>%
select(-all_of(set_cols), -cnt, -na_cols)
test_row_id <- test_df$row_id
test_df <- test_df %>% select(-row_id)On normalise les données :
preProcValues <- caret::preProcess(select(train_basis[-1], -all_of(set_cols)), method = c("center", "scale"))
trainTransformed <- predict(preProcValues, train_df)
validTransformed <- predict(preProcValues, valid_df)
testTransformed <- predict(preProcValues, test_df)
train_mx <- as.matrix(trainTransformed)On définit le modèle avec une couche d’entrée comprenant autant de neurones qu’il y a des variables sans NA, et en couche de sortie autant de neurones qu’il y a de variables avec NA. Ce modèle va donc produire une matrice comprenant une colonne par variable à prédire.
model <- keras_model_sequential() %>%
layer_dense(units = 128, activation = "swish", input_shape = length(train_df)) %>%
layer_batch_normalization() %>%
layer_dense(units = 64, activation = "swish") %>%
layer_dense(units = 32, activation = "swish") %>%
layer_dense(units = 8, activation = "swish") %>%
layer_dense(length(set_cols), activation = "linear")On définit l’optimiseur et on peut compiler le modèle avec comme fonction de perte et métrique “mean_squared_error”.
optimizer <- optimizer_adam(learning_rate = 0.001)
model %>%
compile(
loss = 'mean_squared_error',
optimizer = optimizer,
metrics = "mean_squared_error"
)On peut enfin entrainer le modèle à l’aide de la fonction fit(), en passant en paramètre les données, le nombre d’epochs et la taille du lot. On définit par ailleurs deux fonctions de callback, une pour arrêter l’entrainement s’il n’y a pas d’amélioration (early stopping) et une pour diminuer le taux d’apprentissage si on atteint un plateau (reduce lr on plateau).
model %>% fit(
train_mx,
train_target,
epochs = EPOCHS,
batch_size = BATCH_SIZE,
validation_split = 0.1,
callbacks = list(
callback_early_stopping(monitor='val_mean_squared_error', patience=8, verbose = 1, mode = 'min', restore_best_weights = TRUE),
callback_reduce_lr_on_plateau(monitor = "val_loss", factor = 0.5, patience = 3, verbose = 1)
)
)On fait alors les prédictions sur les données de validation pour évaluer le RMSE sur ces données que l’algorithme n’a pas vu.
pred_valid <- model %>% predict(as.matrix(validTransformed))
predictions_valid <- as.data.frame(pred_valid)
colnames(predictions_valid) <- set_cols
predictions_valid <- predictions_valid %>%
mutate(row_id = row_number()) %>%
pivot_longer(cols = -row_id)
valid_target <- as.data.frame(valid_target) %>%
mutate(row_id = row_number()) %>%
pivot_longer(cols = -row_id)
rmse <- yardstick::rmse_vec(valid_target$value, predictions_valid$value)
print(glue("RMSE - combination {reduce(combi, paste, sep = ", ")}: {rmse}"))Ce qui produit :
...
RMSE - combination F_4_8 F_4_10 F_4_14: 0.296459822230795
RMSE - combination F_4_6 F_4_7 F_4_10: 0.798801761253467
RMSE - combination F_4_0 F_4_2 F_4_13: 0.68729877310422
RMSE - combination F_4_2 F_4_7 F_4_8 F_4_10: 0.727564592227748
RMSE - combination F_4_4 F_4_6 F_4_10 F_4_11: 1.13184400510586
RMSE - combination F_4_1 F_4_9 F_4_10 F_4_11: 0.815886927914656
...Enfin on prédit sur les données de test qui sont les données réellement manquantes, puis on met en forme les prédictions pour ajouter au fichier chaque couple variable / id avec la valeur prédite.
test_predictions <- model %>% predict(as.matrix(testTransformed))
test_predictions <- as.data.frame(test_predictions)
colnames(test_predictions) <- set_cols
test_predictions$row_id <- test_row_id
test_predictions <- test_predictions %>%
pivot_longer(cols = -row_id, names_to = "variable", values_to = "prediction")
predictions <- tibble(`row-col` = glue("{test_predictions$row_id}-{test_predictions$variable}"), value = test_predictions$prediction)
submission <- submission %>% bind_rows(predictions)Conclusion
Voilà ! On vient donc de prédire un million de valeurs manquantes dans une table contenant un million de ligne et 80 variables.
Il y a une différence notable entre la première solution utilisant LightGBM et l’utilisation d’un réseau de neurones multi-sorties, cela étant la première solution nécessite environ 2 heures d’entrainement, alors que la dernière nécessite près de 30 heures (sans GPU). La différence est importante dans le cadre d’une compétition, en pratique peut-être moins, c’est à définir en fonction du problème, et la première solution donne un résultat satisfaisant comparé à une imputation avec la moyenne.
En benchmark, voici le RMSE pour différentes stratégies :
- Imputation avec la moyenne : 0.97937
- LGBM + NN : 0.85xx
- Altération : 0.84xx
- NN multi-sorties : 0.83xx
Savoir comment imputer les valeurs manquantes est utile pour pouvoir effectuer une analyse malgré l’absence de certaines données, ce qui est un problème très fréquent en pratique.
Références
Ma solution pour la compétition: https://github.com/cnicault/tabular-playground-series/tree/main/Jun-2022
Compétition sur Kaggle: https://www.kaggle.com/competitions/tabular-playground-series-jun-2022/data